ग्राफीय विधि द्वारा गति के समीकरण (Equations of Motion by Graphical Method)
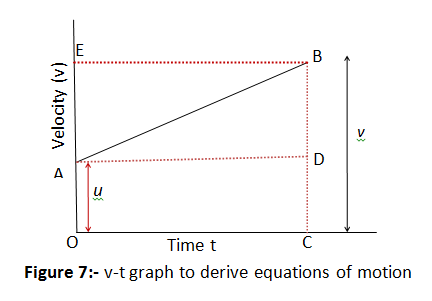
मान लिया कि एकसमान त्वरित गति से चल रहे एक वस्तु का ग्राफ निम्नांकित है।
इस ग्राफ में,
प्रारंभिक वेग =u(u≠0) [ A बिन्दु पर]
अंतिम वेग =v [ B बिन्दु पर]
मान लिया कि समय t में वस्तु का प्रारंभिक वेग u से बद्लकर v हो जाता है।
अर्थात समय =t
अब बिन्दु B से दो लम्ब BC तथा BE क्रमश: समय तथा वेग अक्ष पर डाला गया।
अत: OA द्वारा प्रारम्भिक वेग तथा BC द्वारा अंतिम वेग दर्शाया गया है।
तथा समयांतराल t को OC द्वारा दर्शाया गया है।
ग्राफीय विधि द्वारा वेग तथा समय के संबंध का समीकरण
BD = BC – CD
यह समयांतराल t में वेग में परिवर्तन दर्शाता है।
अब AD को OC समांनांतर खींचा गया
अत: ग्राफ के द्वारा
BC = BD + DC
⇒BC=BD+OA
अब BC =v तथा OA =u का मान रखने पर
v=BD+u
⇒BD=v−u -----------(iv)
अब हम जानते हैं कि इकाई समय में वेग में परिवर्तन त्वरण (a) होता है।
अत:

⇒a=BDAD
[जहाँ a = त्वरण]
⇒a=BDOC
अब OC = t रखने पर हम पाते हैं कि
⇒a=BDt
⇒BD=at ------------(v)
अब समीकरण (iv) में BD का मान रखने पर
v=u+at ------------- (vi)
जहाँ u= प्रारम्भिक वेग, v=अंतिम वेग, a = त्वरण तथा t= समय
यह समीकरण (vi) वेग–समय संबंध के लिये समीकरण कहा जाता है।
अत: u,v,a तथा t में से किसी तीन का मान ज्ञात होने पर चौथे राशि के मान की गणना की जा सकती है।
ग्राफीय विधि से समय–स्थिति संबंध के लिये समीकरण
मान लिया कि एक वस्तु ने एकसमान त्वरण a से t समय में s दूरी तय करती है।
अत: दिये गये ग्राफ में वस्तु द्वारा तय की गई दूरी, वेग–समय ग्राफ AB के नीचे घिरे क्षेत्र OABC द्वारा प्राप्त की जाती है।
∴ s = OABC का क्षेत्रफल
= समलम्ब चतुर्भुज OADC का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल
=OA×OC+12(AD×BD)
अब चूँकि OA = u तथा OC = AD =t तथा BD = at
अत: OA, OC, AD तथा BD का मान रखने पर हम पाते हैं कि
s=u×t+12(t×at)
⇒s=ut+12at2 --------- (vii)
यह समय–स्थिति के लिये समय कहलाता है।
दिये गये समय–स्थिति में s,u,t तथा a में से किन्हीं तीन का मान ज्ञात रहने पर चौथे का मान ज्ञात किया जा सकता है।
वेग –स्थिति संबंध के लिये समीकरण (Equation for Position Velocity Relation)
वस्तु के द्वारा एकसमान त्वरण a से t समय में तय की गई दूरी को ग्राफ के नीचे समलम्ब चतुर्भुज OABC द्वारा घेरे गये क्षेत्रफल द्वारा प्रदर्शित किया गया है।
अर्थात, दूरी, s = समलम्ब चतुर्भुज OABC का क्षेत्रफल
= 12(समानांतर भुजाओं का योग)× समानांतर भुजाओं के बीच की दूरी
=12(OA+BC)×OC
अब OA =u, BC =v तथा OC =t, का मान रखने पर हम पाते हैं कि
s=12(u+v)t ----------- (viii)
अब, वेग–समय संबंध से हम जानते हैं कि
v=u+at
⇒at=v−u
=t=v−ua
अत: उपरोक्त t का मान समीकरण (viii) में रखने पर हम पाते हैं कि
s=12(u+v)×v−ua
⇒s=12a(v2−u2)
[∵(u+v)(u−v)=v2−u2]
=2as=v2−u2
⇒v2=u2+2as ------------ (ix)
इस समीकरण को वेग –स्थिति संबंध समीकरण कहा जाता है।
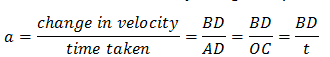
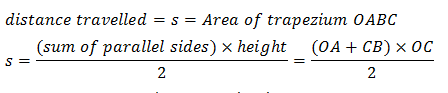
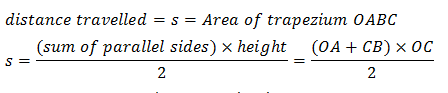
Comments
Post a Comment